Sokszor vita tárgya a távcső felbontása, hogy mit lehet látni vele és mit nem.
Van egy egyszerű számítás amellyel gyorsan megkapható, hogy mire számítsunk.
Egyik megfontolás szerint 115-öt, másik szerint 138-at, osztjuk a főtükör mm-ben mért átmérőjével és megkapjuk a távcső ív másodpercben mért felbontóképességének alsó határát.
Például van egy 114 mm átmérőjű főtükörrel rendelkező Newtonunk, akkor
115/114 = 1,008772 " az a legkisebb szög ami alatt látható-elkülöníthető két pont.
Ez mit jelent?
A Jupiter amikor júniusban közel volt 45" (ívmásodperc) alatti szögben látszott.
Azaz egy példabeli távcsővel 45 "csíkra bontható fel a képe.
ÉS ! ! !
Azok a pontjai amik között a szögtávolság kisebb volt mint 1", azok bizony összeolvadtak közös folttá.
Ezért egy ilyen távcsővel maximum a két nagy felhősáv csíkja különül el, akármekkorára is nagyítjuk a képet. Újabb részletet nem fogunk látni.
Ezt a 115/114-et hívjuk tiszta nagyításnak, az ugyanezen arányú távcsöveknél a nyújtókkal ( Barlow-ok és fókusznyújtók) és/vagy pici fókusztávolságú okulárokkal (szemlencsékkel) sokszorosára növelhetjük a nagyítást, de a részletek száma marad.
Az ilyen nagyítást éppen ezért "üres" nagyításnak nevezzük. Mert nem ad újabb részleteket.
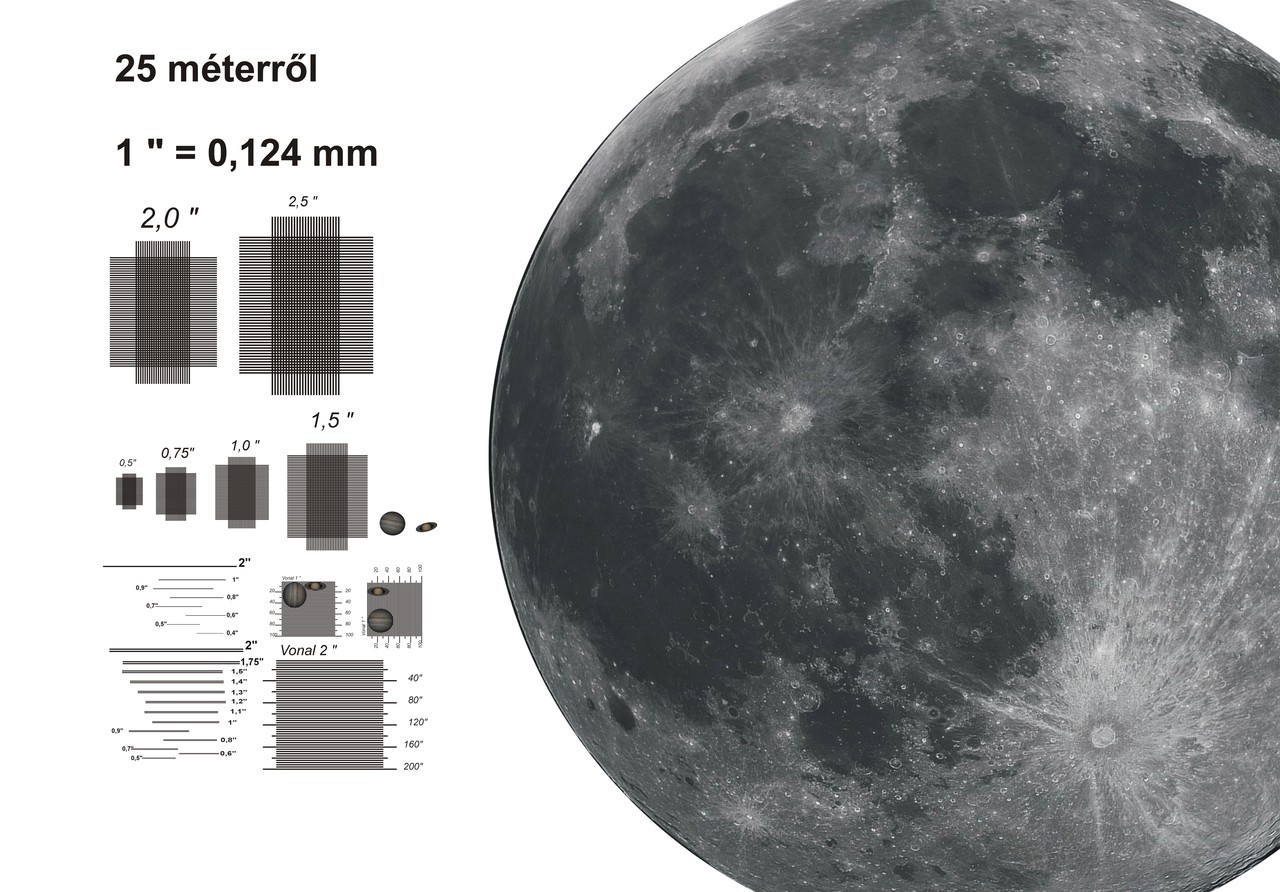
Itt egy ábra, amit 25 méterről nézve, (célszerűen 100-szoros nagyításnál éppen úgy látjuk, mint szabad szemmel 25 centiről, lévén 1 m=100 cm ) a ráírt ívmásodpercek alatt látszanak a csíkok.
Így gyorsan ellenőrizhetjük, hogy a távcsövünk hozza-e a papírformát, vagy cserélni kell valamelyik elemét, mert gyengébb a "teljesítménye" azaz nem látjuk azt amit látnunk kellene. Példaként az említett távcsővel nem látszik különállónak az 1" jelzésű két vonal.
Egy dolgot még érdemes tudni erről a felbontóképességről!
Két, egymás melletti pontra vonatkozik. Azaz ha ugyanezzel a határ felbontással nézünk például egy fűszálat, akkor tízszer nagyobb távolságból is látszik, ha elüt a háttértől, még úgy is, hogy ekkor már tízszer kisebb látószög alatt látjuk.
Azt ugye tudjuk, hogy a látószög a távolsággal arányos, azaz kétszeres távolságnál felére csökken.
Így ha például 1 km távolságról nézünk egy 10 m magas oszlopot, akkor kétszer magasabbnak látjuk, mint akkor ha ugyanezt az oszlopot 2 km távolságról néznénk.


Ajánlott bejegyzések:
A bejegyzés trackback címe:
Kommentek:
A hozzászólások a vonatkozó jogszabályok értelmében felhasználói tartalomnak minősülnek, értük a szolgáltatás technikai üzemeltetője semmilyen felelősséget nem vállal, azokat nem ellenőrzi. Kifogás esetén forduljon a blog szerkesztőjéhez. Részletek a Felhasználási feltételekben és az adatvédelmi tájékoztatóban.